SSO – Sports Strategy Optimization
Project Leader: Prof. Dr. Jörg Rambau
Contact: Prof. Dr. Jörg Rambau
Project start: 2012/10/01
Project team:
- Prof. Dr. Jörg Rambau
- M. Sc. Susanne Hoffmeister
- Prof. Dr. Andreas Hohmann
- Ronan Richter M.Sc.
Project description:
APPLICATION BACKGROUND
In sports games, the strategic preparation of a team dependent on the opponent can have a strong influence on its success. For example, in beach volleyball it may be advantegeous to play very risky against a team with enormous attack skills whereas it may be more successful to keep the ball in play as long as possible against a team making relatively many unforced errors. We want to decide based on individual players' skills in the teams which out of two strategies has the larger winning probability. In order to sync the premises, the data collection, and the interpretation of results with expertise from sports sciences, the Lehrstuhl Wirtschaftsmathematik (Prof. Dr. Jörg Rambau) cooperates in this project with the Lehrstuhl Sportwissenschaften I (Prof. Dr. Andreas Hohmann).
CONTRIBUTION TO THE MISSION OF MODUS
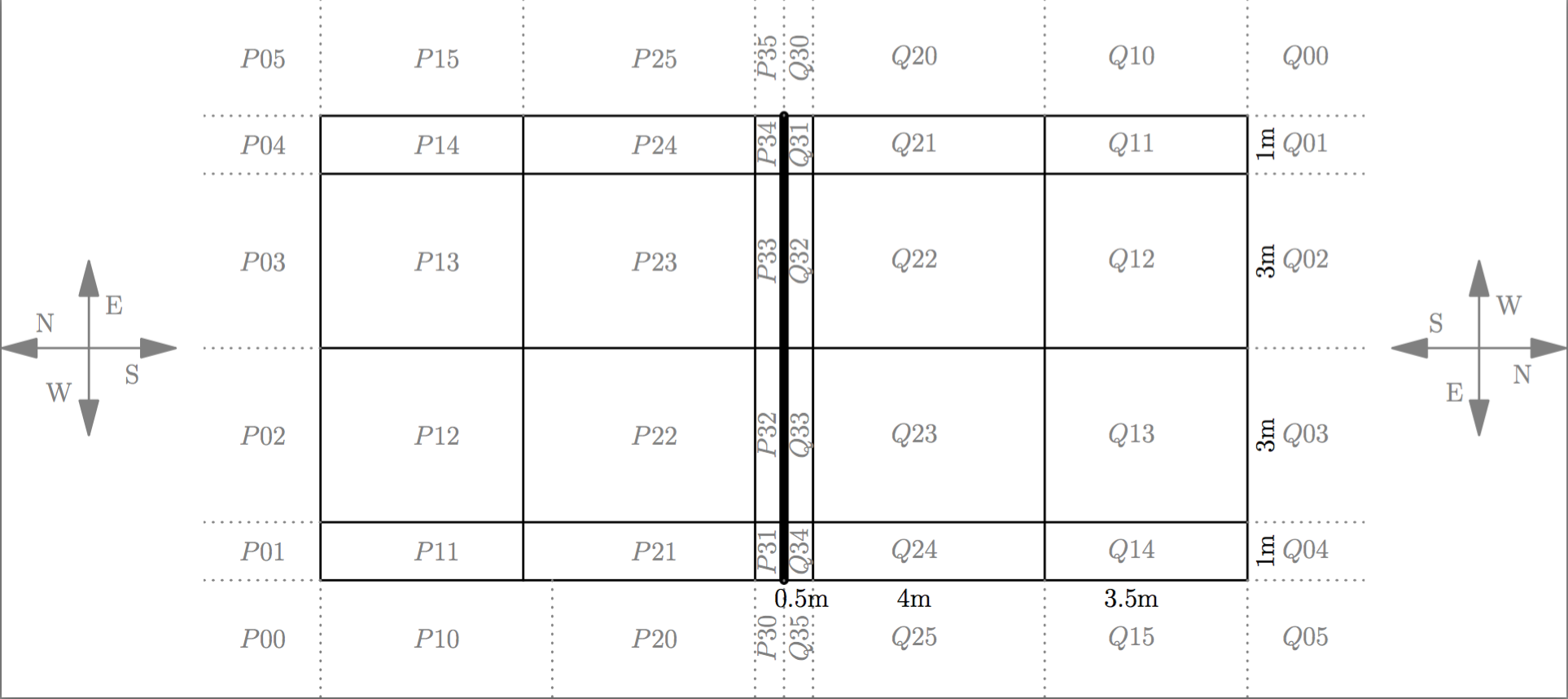
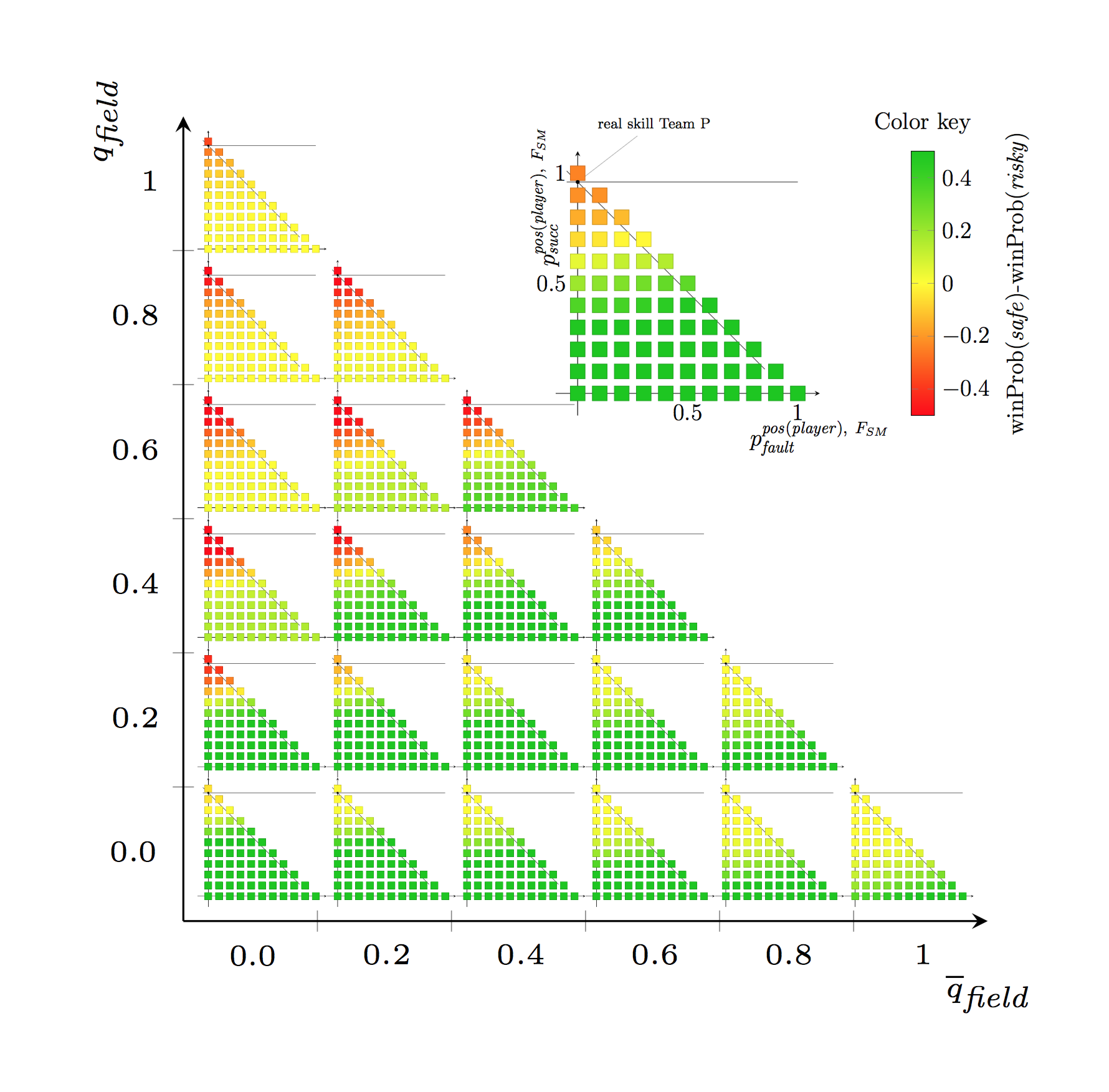
Whereas so far mainly Markov chains have been utilized to formalize the dynamic system of a sports game, we formalize the game by means of Markov Decision Problems (MDP). The players' skills influence the success probabilities of certain actions. Multiple actions (depending on a state of the game) are aggregated to a strategies. The winning probability of a strategy (i.e., play risky or play safe) is analyzed in the coarsets possible MDP (the strategic MDP or the s-MDP) that can express the strategy. States are represented by, e.g., the current score, the right to serve, etc. Whenever the state is a terminal state for the game, the system remains in that state with no further profit. The profit of a winning state (i.e., the score is so that we have won) is set to one, the score of a losing state to zero. This way, the expected total profit of a policy equals the winning probability. And the expected total cost can be investigated by analyzing the MDP. We found it convenient to provide another, more detailed MDP (the game-play MDP or the g-MDP) in order to make the estimation of the state transition probabilities only dependent on individual players' skills and not on the pairing of teams. This formalizes an estimator for the point winning probabilities based on simulation in the g-MDP parametrized by individual players' skills.
RESULTS
The project team could characterize optimal policies for the s-MDP for beach volleyball whenever the skills do neither depend on the duration of the game nor on the score. The olympic games in London 2012 were analyzed in hindsight based on manual video data extraction to find out evidence for why the german team won the final. Meanwhile (end of 2018), Susanne Hoffmeister has submitted her PhD. thesis about this activity and the underlying theory of MDPs.

